A Linear Time Solution To Advent of Code Day 8
A few weeks ago I tried to go through Advent of Code 2020 (spoiler I didn't finish). Advent of Code is a set of 25 coding challenges each with two parts. The challenges are unveiled one at a time from the beginning of December until Christmas day.
One fun thing about Advent of Code is that everyone does it differently. People write solutions in every language out there (and some new ones they've invented) using many different techniques (I'm sure there's someone who tries to do the whole thing in regex).
I found part 2 of problem 8 to be very interesting and wanted to write up my solution.
A Quick Summary of the Problem
Part 2 of day 8 basically boils down to the following:
We have a very simple machine. Initially there is a program counter, which starts at the beginning of the program, and a single global counter, which starts at 0. At each step, the instruction that the counter is pointing to is executed. There are 3 different instruction types each taking an integer parameter:
- jmp arg, increments the program counter by arg
- add arg, adds arg to a global counter and increments the program counter by 1
- nop arg, increments the program counter by 1. It does not use its argument but it still takes one
If the counter ends up pointing one index past the last instruction, the program ends and returns the global counter value.
Here's an example program:
0: nop +0
1: acc +1
2: jmp +2
3: acc +5
4: acc +2
This program returns 3.
What about this program?
0: nop +0
1: acc +1
2: jmp +4
3: acc +3
4: jmp -3
5: acc -99
6: acc +1
7: jmp -4
8: acc +6
It never ends! If we trace the execution of this program, we will find out we are actually stuck in an infinite loop!
In this problem, we can assume any looping program we encounter can be fixed by changing either a nop to a jmp or a jmp to a nop in exactly one place. Importantly the argument to the flipped jmp / nop does not change. In the above program changing instruction 7 to a nop will fix the program, allowing it to terminate with a value of 8.
Our task is to take in a looping program, find the one flipped instruction, change it and get the return value of the terminating program.
The Simple Solution:
One simple thing we could do to find the solution is to try to flip each jmp and nop instruction, one at a time, and rerun the entire program after each flip. One of the flips is guaranteed to make the program stop looping and we will just return the result from that run. This solution is both straightforward and solves the problem which makes it a great solution. Algorithmically it runs in O(number of instructions^2) because we must run the entire program once for every instruction we flip.
However in the spirit of doing each challenge in different ways I wondered if this problem could be done faster?
An Edgy Approach
Another way to think of these programs is as directed graphs. Each node represents an instruction and has an edge pointing towards the next executed instruction.
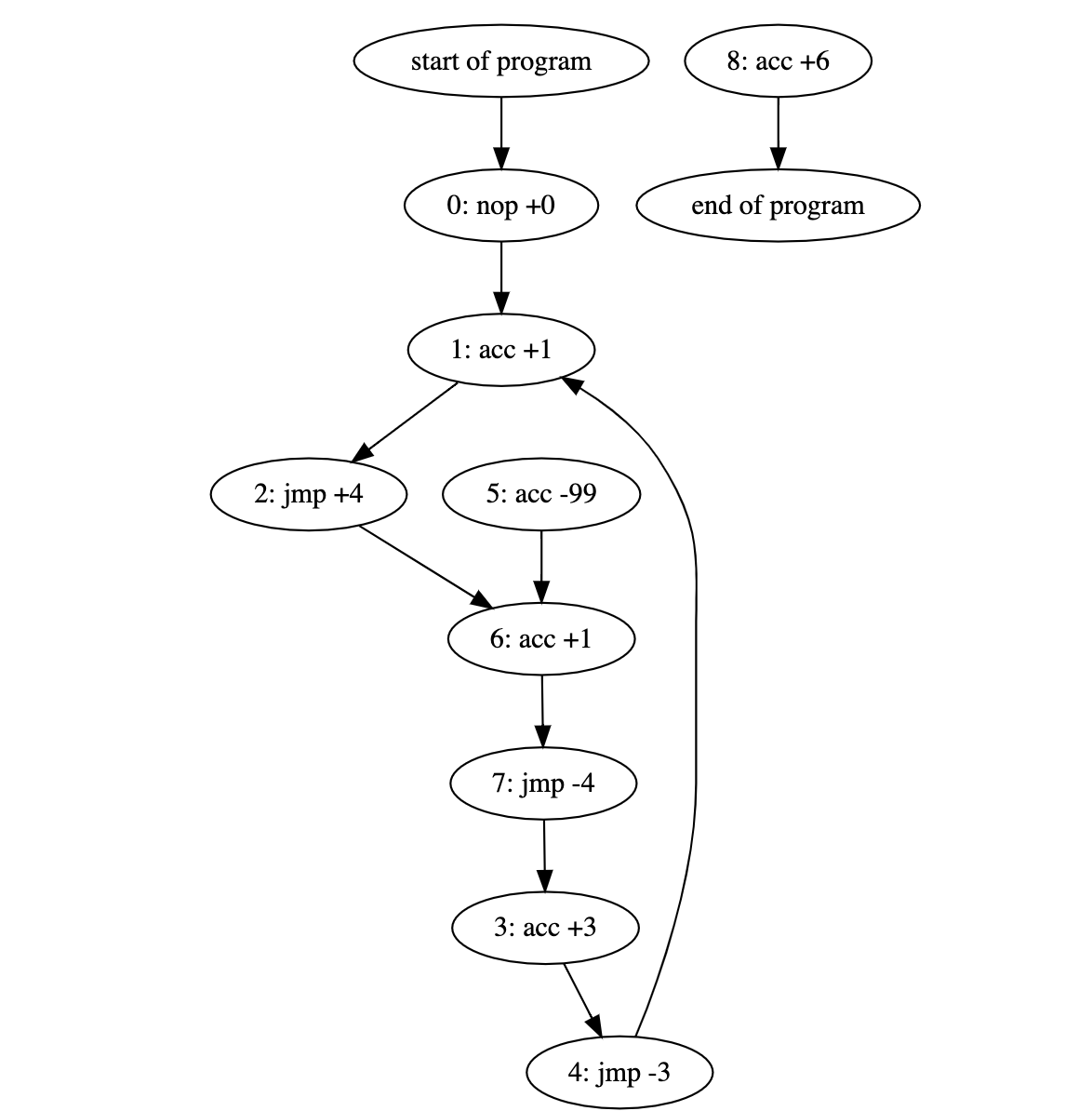
I've now marked every instruction in the initial loop as red.
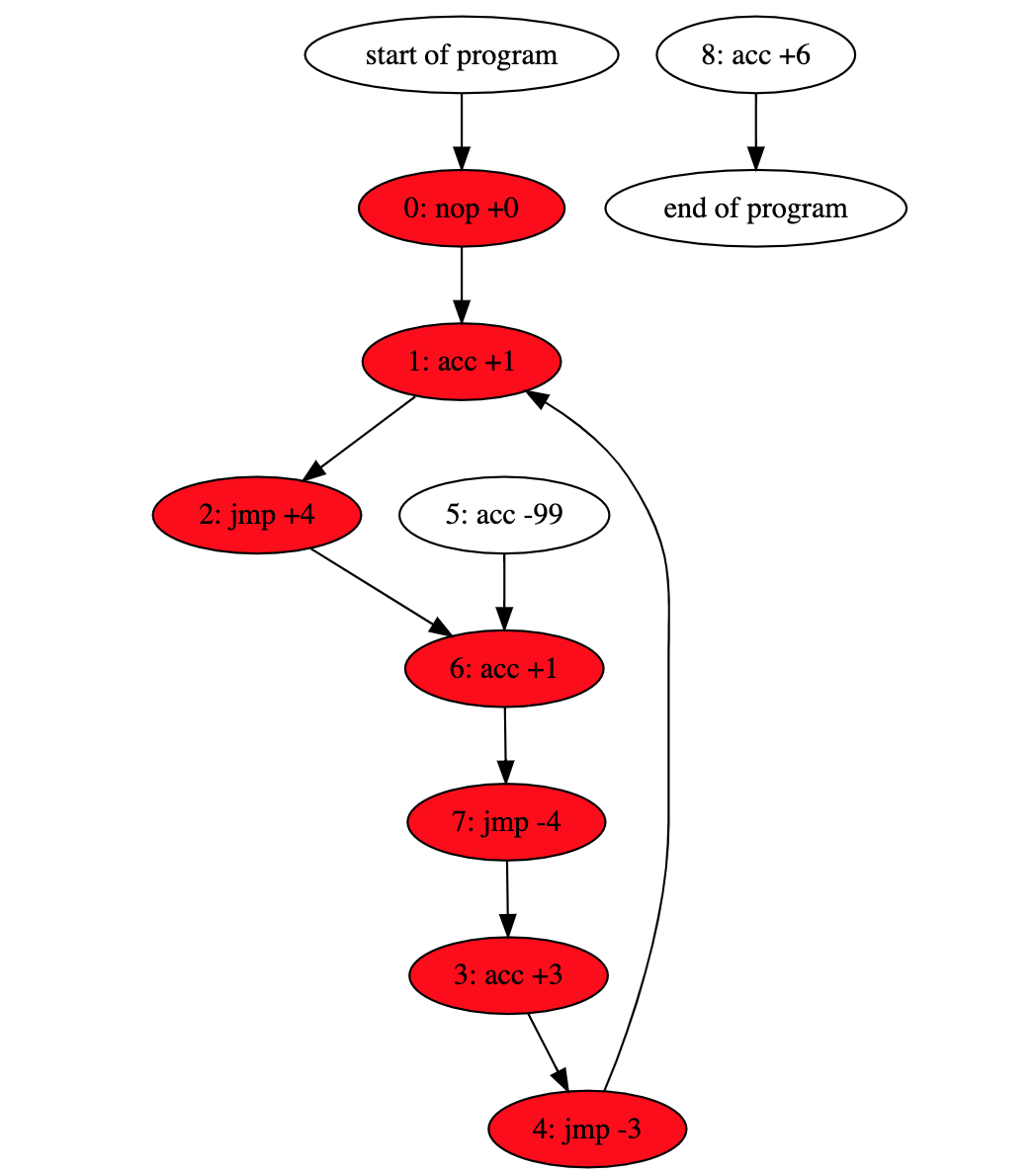
A quick but important fact is that the instruction that we need to flip must be in the initial loop. So it must be one of these original red instructions.
Now we are going to try to flip each of the red jmp / nop these instructions one by one and check each time to see if the modified program terminates.
What?! Isn't that exactly what we did in the N^2 solution above? It turns out the difference will be not in the number of instructions we try to flip, but how we check for program termination.
Before we start our algorithm, let's create a set called cyclic_nodes. This is a subset of all the nodes which are guaranteed to connect to a cycle in the unmodified graph. Initially this set will contain all the red nodes in the first loop.
Now let's try flipping one of our red jmp / nop nodes (call it Node A). That node's edge now points somewhere else in the graph (Node B). There are two cases here:
- Node B is already in cyclic_nodes. This means that we are guaranteed to get stuck in a cycle so we can know Node A isn't the correct node to flip. To see why consider these two sub cases:
- There is a path from Node B to Node A. In this case we know we are still in a cycle. We know this because even though the graph has been modified, the only modification is to the edge leaving Node A so none of the nodes on the path from B to A will have been changed.
- There is a path from Node B to a different cycle. By similar logic to the first part, since no node on that path or in that cycle has been modified the program will loop.
- Node A points to a node not yet in cyclic nodes. In this case we follow the path until we either hit a node in cyclic nodes, loop in a never before seen cycle, or hit the end of the program.
- If we hit the end of the program we have found the instruction to flip and we are done
- In the other two cases we have entered a cycle. Add all nodes we walked over to the cyclic_nodes set and move to the next instruction.
What is the runtime of this algorithm? Well we only go over each potential switch once. However unlike the simple algorithm, we also know during the check for cycle step each node is only added to the cyclic_nodes set once. Therefore the runtime is linear with respect to the number of instructions.